
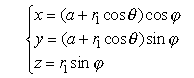

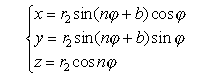


Kwadreerbaar betekent dat je de oppervlakte bij gegeven straal van de halve bol met passer en liniaal moet kunnen construeren.
Het is een pseudo-architectonisch probleem: de oppervlaktebepaling van een koepelgewelf.
Viviani loste het probleem op door de halve bol te doorsnijden met twee halve cilinders (in Rhino heet deze bewerking Boolean difference). Het oppervlaktestuk boven de cilinders noemde Viviani Vela Quadrabile Fiorentina.
Hiernaast is een en ander weergegeven met behulp van een gehele bol.
De gemeenschappelijke (snij)kromme is een ruimtekromme in de vorm van twee 8-en (gelegen op de bol). Zo'n achtje heet "kromme van Viviani".
De oppervlakte van de "vela" is 4R2 (R is de straal van de bol).


De Wig van Wallis ontstaat uit een cirkel met diameter d en een lijnstuk met lengte d, waarvan het midden loodrecht ligt boven het middelpunt van de cirkel, en wel op hoogte d.
De beschrijvenden van de wig zijn alle evenwijdig aan het middelloodvlak van het lijnstuk en verbinden een punt van het lijnstuk met een punt van de cirkel.
De doorsneden van de wig met een vlak evenwijdig aan het vlak van de cirkel zijn ellipsen (tja, ook een lijnstuk is een, weliswaar gedegenereerde, ellips).
De sphericon (wobbelding, wobbelbol) is een ruimtelijk lichaam dat is afgeleid van een dubbelkegel, waarvan de beide tophoeken gelijk zijn aan 90°.
Het diagonaalvlak door de toppen snijdt de dubbelkegel in twee delen, met als doorsnede een vierkant. Het ene deel van de figuur wordt dan om het middelpunt geroteerd over een hoek van 90° met als resultaat de sphericon.
De sphericon heeft een continu oppervlak. Het lichaam rolt door te "wobbelen" over de twee (tov. elkaar gedraaide) helften, hetgeen resulteert in een beweging volgens een rechte lijn.